Teoria

[ Home ] [ Su ]

Teorema di Steiner
Il momento d’inerzia di un corpo rigido di massa M rispetto ad un asse parallelo ad un asse baricentrale è uguale alla somma del momento d’inerzia rispetto all’asse baricentrale aumentato del prodotto della massa M per il quadrato della distanza dell’asse considerato dall’asse baricentrale. In simboli Il simbolo I_CM indica il momento d’inerzia del corpo rispetto all’asse baricentrale parallelo all’asse a. Il baricentro di un corpo è denominato anche centro di massa e la sua determinazione per un corpo generico implica una certa difficoltà. Solo per le figure che presentano qualche simmetria l’individuazione del punto geometrico può essere agevole. In generale occorre il calcolo integrale ad un livello la cui trattazione non rientra nei normali programmi di matematica della Scuola Secondaria Superiore.	Fig.1
	Fig.2
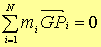
Dimostrazione del teorema (Caso di un corpo bidimensionale) Per la dimostrazione della formula consideriamo in un primo momento una lamina piana di forma qualsiasi della quale indichiamo con G il centro di massa. Ricordiamo che per un sistema discreto di particelle il centro di massa è definito come il punto G dello spazio che verifica l’equazione vettoriale Al fine di rendere più facilmente comprensibile la dimostrazione che presentiamo supponiamo di considerare il corpo rigido come formato da N masse puntiformi: m₁, m₂,m₃,.., m_N. Fissiamo un sistema di riferimento cartesiano ortogonale xOy nel piano contenente il corpo laminare C e sia a l’asse perpendicolare a detto piano e passante per il punto Q di coordinate (x_Q;y_Q). Consideriamo la massa elementare m_i nella posizione P_i . 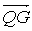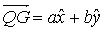Per il vettore supponiamo che si abbia con 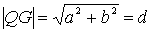; consideriamo infine il vettore 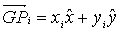. La distanza della massa elementare m_i dall’asse a è data evidentemente dal modulo del vettore 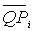espresso da per cui il suo momento d’inerzia rispetto a detto asse è Per determinare il momento d’inerzia del corpo rispetto all’asse a dobbiamo sommare tutti i momenti d’inerzia elementari delle masse m_i . 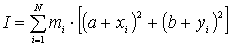Otteniamo perciò Sviluppiamo i quadrati presenti e raccogliamo adeguatamente i termini. 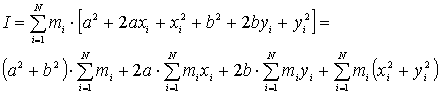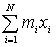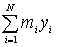Notiamo ora che dalla proprietà del centro di massa risultano nulli i due termini centrali , inoltre il primo termine rappresenta il prodotto della massa del corpo per il quadrato della distanza d fra l’asse a e l’asse ad esso parallelo passante per il centro di massa , mentre l’ultimo termine rappresenta il momento d’inerzia del corpo rispetto all’asse baricentrale. Abbiamo dunque ottenuto la relazione prevista dal teorema di Steiner nel caso considerato. torna su (Caso di un corpo tridimensionale) La validità del teorema di Steiner anche nel caso tridimensionale si può provare pensando di “affettare” il corpo con tanti piani paralleli tra loro e perpendicolari all’asse a rispetto al quale s’intende determinare il momento d’inerzia. E’ evidente che per ciascuna di tali sezioni il teorema è già acquisito e per avere il momento d’inerzia complessivo basta sommare i momenti d’inerzia rispetto allo stesso asse di tutte le singole fette. 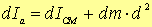Se indichiamo con dm la massa di ciascuna di queste fette possiamo scrivere la relazione di Steiner nel modo seguente con l’ovvio significato dei simboli. Effettuando quindi la somma di tutti i momenti d’inerzia elementari dI_a con il calcolo integrale si perviene agevolmente al risultato indicato dal teorema giacché il calcolo dell’integrale del primo termine fornisce il momento d’inerzia del corpo rispetto all’asse baricentrale e nel calcolo dell’integrale del secondo termine, essendo costante il fattore d² , si tratta solo di sommare tutte le masse delle “fette” e quindi si ricava la massa M complessiva del corpo. Il teorema è così acquisito per un corpo qualsiasi. torna su